State-Space workshop. Welcome!
Link to repo: https://github.com/QuinnAsena/state-space-workhop-ESA
UW-Madison
2024-08-05
Go here! 👇
Link to repo: https://github.com/QuinnAsena/state-space-workhop-ESA
State-space modelling
One of the primary goals of this model is to be able to test multiple hypotheses about the data and lend statistical support to the different hypotheses.
This state-space approach allows us to estimate coefficients for taxa interactions and driver-taxa relationships, that we don’t get from methods such as ordination or cluster analysis.
We recommend this method as complimentary to other methods, as both have their advantages.
Work with uneven time-intervals between observations, and multinomially distributed data
Today’s objectives
- Learn the data structure for
multinomialTS - Understand how to fit
multinomialTS- Finding starting values with
mnGLMM() - Fitting
mnTS()
- Finding starting values with
- Fit
mnTS()to multiple hypotheses - Assess resulting models
Multinomial and relative abundance data \(Y\)
- Multinomial distribution models the probability of counts for each side of a \(k\)-sided dice rolled \(n\) times
- Individuals counted from each of \(k\) species when \(n\) counts total are made
- Relative abundace data mean we can generate estimates for \(n-1\) taxa
- Everything is estimated against a reference group

The data
The response variable, \(Y\), is of count-type data. Covariates, \(X\), can be of mixed types (e.g., binary events, or charcoal accumulation rate).
For the model we need two matrices of data:
- \(Y =\) Count data (e.g., pollen, diatoms…)
- \(X =\) Matrix of covariates
Estimated effects
Today, we will look into the estimated parameters \(B\) and \(C\):
- \(B =\) Covariate effect
- \(C =\) Species interactions
Fitting the model to estimate different combinations of parameters allows us to test hypotheses and lend statistical support to them.
For example are species interactions or environmental covariates the primary driver or change?
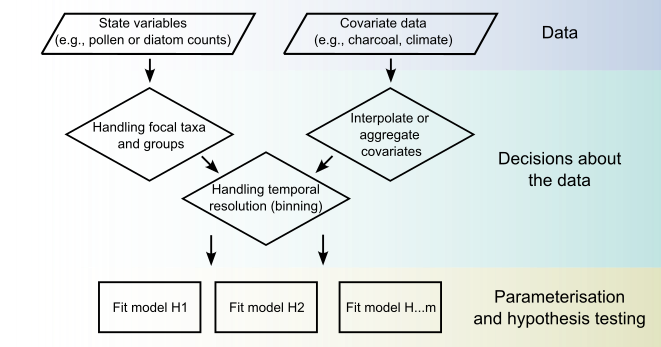
Decisions about the data
- Key taxa and groups
- Prediction resolution
- Parameters to estimate
Key taxa and groups
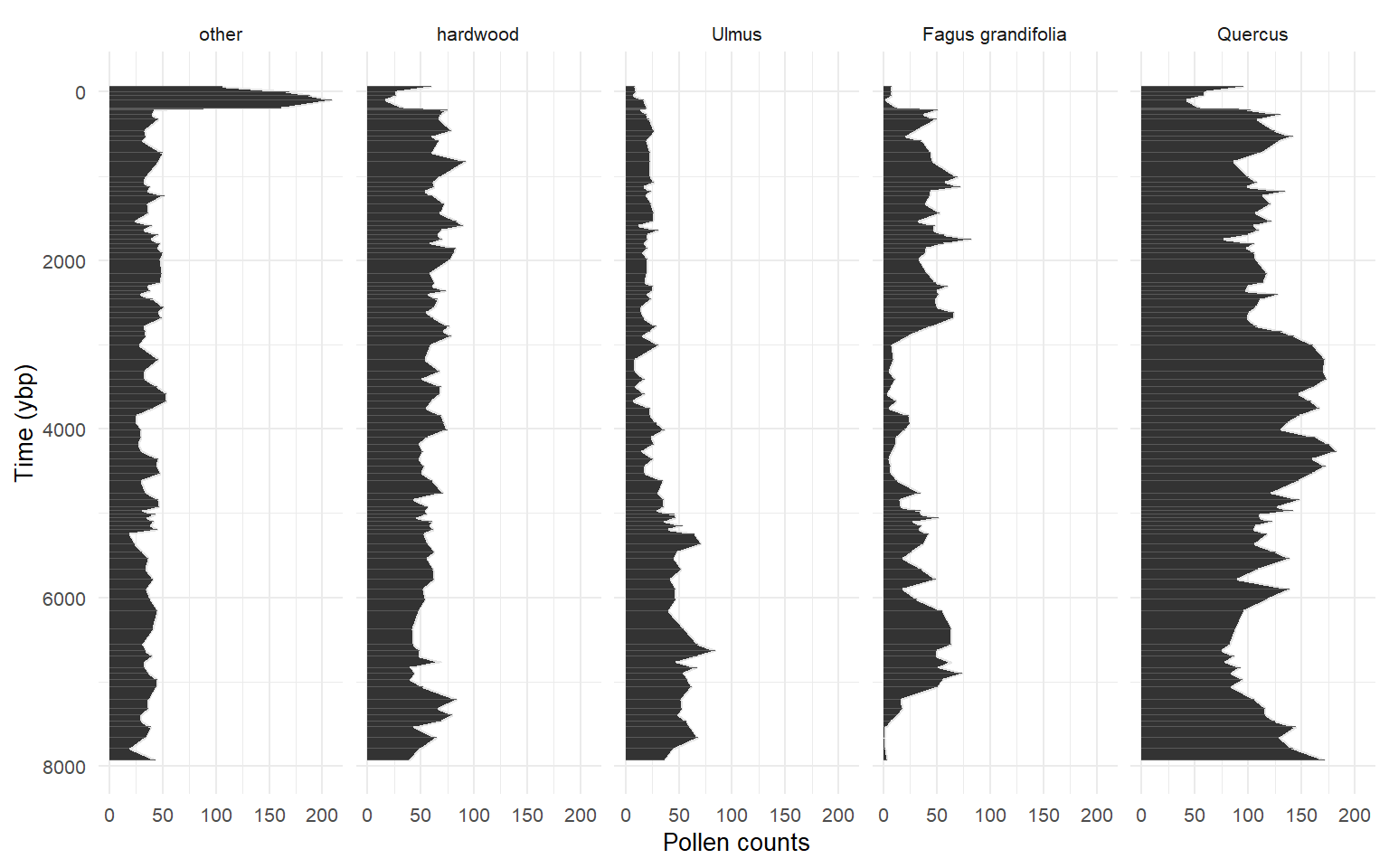
- Generating estimates for all matrices for large numbers of taxa is problematic
- so we focus on key groups or taxa, and sum the remaining taxa into the reference group.
- We are going to use Story Lake as an example in this workshop.
Sroty Lake
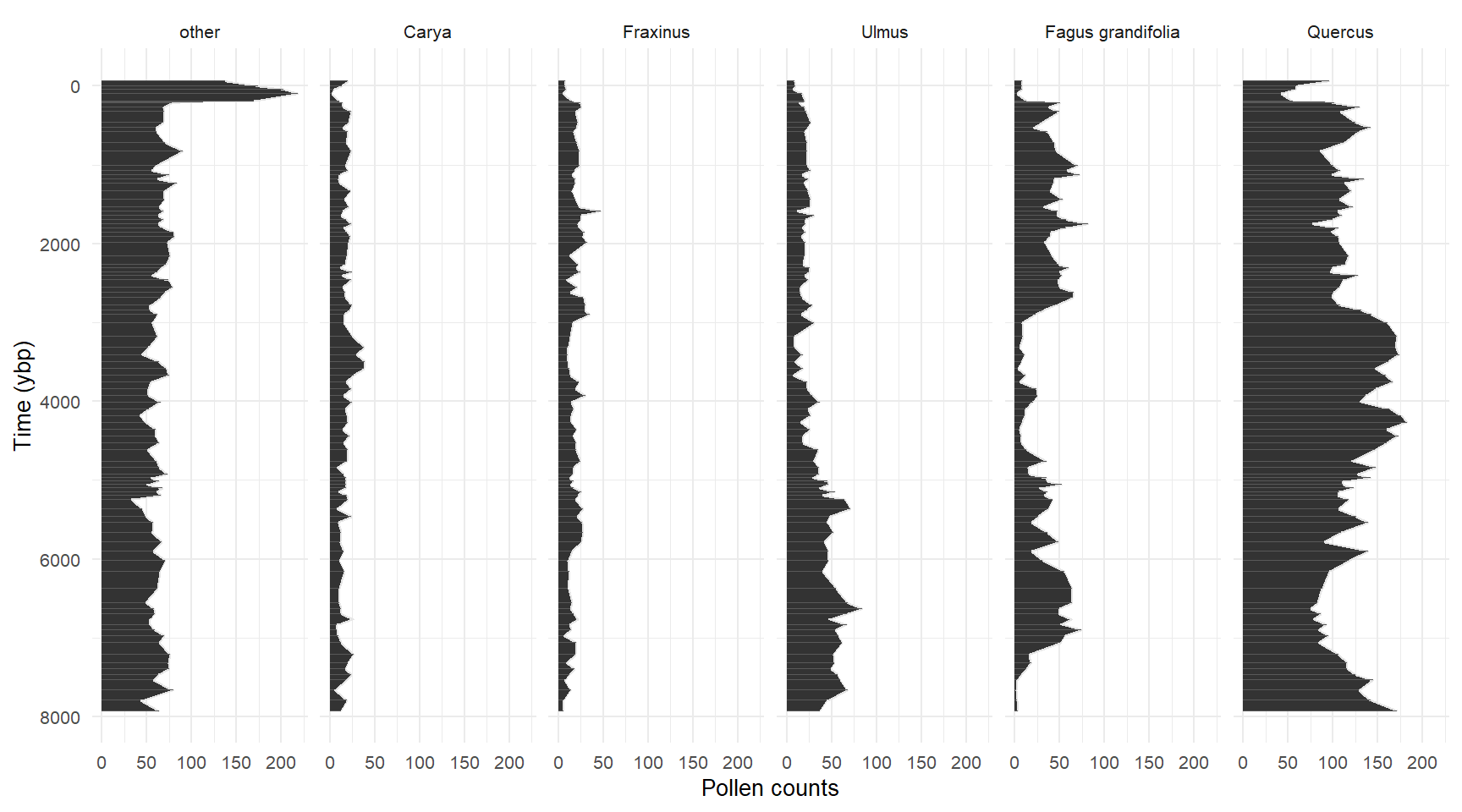
Story lake grouped
Prediction resolution
- The model will make predictions at a chosen resolution: e.g., every 50, or 100 years.
- We need to choose a resolution those predictions
- for palaeo-data we don’t attempt to make annual predictions from say 100 observations over 13,000 years, but in 50-100 year bins.
Parameters to estimate
- We also make decisions aroun which parameters to estimate
- e.g., which interactions among taxa
Fitting the model to different combinations of parameters and assessing the resulting models lends statistical support to hypotheses about the data.
Key points
- Response variable \(Y\) is multinomially distributed
- Covariate \(X\) may be of mixed types
- Key taxa and groups are chosen
- A prediction resolution is chosen
- Fit the model to different combinations of parameters to test alternative hypotheses
Go here! 👇
Link to repo: https://github.com/QuinnAsena/state-space-workhop-ESA
Fitting process